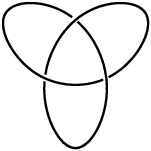
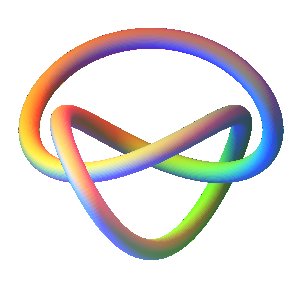Trefoil Knot

A loop with 0 crossings is the unknot.

Trefoil knot. The trefoil knot also called the threefoil knot or overhand knot is the unique prime knot with three crossings. It can be obtained by joining the loose ends of an overhand knot. 15 2 x 2 x 0 065 square tubing 3 2 x 1 8 flat bar 2 x 1 wood slab 1 flap disc 1 can flat black paint. A little thought should convince you that there are no knots with fewer than three crossings.

The trefoil knot fold is a protein fold in which the protein backbone is twisted into a trefoil knot shape. In fact b is arguably the simplest true knot known as the trefoil or overhand knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot resulting in a knotted loop. The trefoil can be obtained by joining together the two loose ends of a common overhand knot resulting in a knotted loop.

A knot diagram of the trefoil knot the simplest non trivial knot in topology knot theory is the study of mathematical knots. Mathematically it can be described in many variants. In knot theory a branch of mathematics the trefoil knotis the simplest example of a nontrivial knot. As the simplest knot the trefoil is fundamental to the study of mathematical knot theory.

As the simplest knot the trefoil is fundamental to the study of mathematical knot theory which has diverse applications in topology geometry physics and chemistry. A diagram with exactly 1 crossing can be simplified using reidemeister move i and hence is equivalent to the unknot. In knot theory a branch of mathematics the trefoil knot is the simplest example of a nontrivial knot. In knot theory a branch of mathematics the trefoil knot is the simplest example of a nontrivial knot.

The trefoil and its mirror image are not equivalent as first proved by dehn 1914. In topology a branch of mathematics the trefoil knot is the simplest example of a nontrivial knot. As the simplest knot the trefoil is fundamental to the study of mathematical knot theory. The trefoil can be obtained by joining together the two loose ends of a common overhand knot resulting in a knotted loop.

In other words the trefoil knot is not amphichiral. In knot theory the trefoil knot is the simplest nontrivial knot. The trefoil knot is named after the three leaf clover plant. While inspired by knots which appear in daily life such as those in shoelaces and rope a mathematical knot differs in that the ends are joined together so that it cannot be undone the simplest knot being a ring or.

A trefoil knot is the unique prime knot with three crossings. The trefoil knot is named after the three leaf clover or trefoil plant. The trefoil can be obtained by joining together the two loose ends of a common overhand knot resulting in a knotted loop.